Zajímavosti

Popularita přechodu Venuše přes sluneční disk je vskutku značná. Svědčí o tom úloha z loňského ročníku 1. kola fyzikální olympiády v kategorii C:

Zadání úlohy FO 44 - C - I - 4

Dne 8. června 2004bude při pozorování ze Země přecházet planeta Venuše přes sluneční disk. Pro zjednodušení předpokládejme, že Země a Venuše obíhají kolem Slunce po kružnicích v téže rovině.

1. Určete poměr zorných úhlů, pod kterými v uvedené době uvidíme průměr Venuše a průměr Slunce.
2. Určete dobu trvání přechodu středu Venuše přes sluneční disk.
3. Stanovte datum, kdy mohlo dojít k předcházejícímu přechodu, pokud by byl splněn výše uvedený zjednodušující předpoklad.
4. K přechodu ve skutečnosti naposledy před uvedeným datem došlo 6. prosince 1882. Zdůvodněte, proč k jevu nedochází tak často, jak vychází z předcházejících výpočtů.

Řešení úlohy FO 44 - C - I - 4

Zaveďme označení údajů nalezených v tabulkách:
průměr Slunce D = 1 391 000 km, průměr Venuše d = 12 100 km,
střední vzdálenost Země od slunce r₀ = 1 AU = 149 600 000 km,
střední vzdálenost Venuše od Slunce r = 0,7233 AU,
periodu oběhu Země T₀ = 365,24 d a periodu Venuše T = 224,7 d.

1. Průměry Venuše a Slunce uvidíme v době přechodu pod zornými úhly α₁ = d / (r₀ – r), α₂ = D / r₀. Hledaný poměr je α₁ / α₂ = r₀d / ((r₀ – r)D) = 0,031.
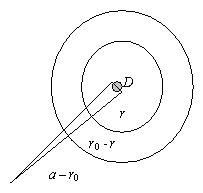
2. Označme a vzdálenost od Slunce, ve které se nachází průsečík přímek spojujících středy obou planet na začátku a na konci přechodu. Dále označme v₀, v po řadě kruhové rychlosti, se kterými obíhá Země a Venuše kolem Slunce a Δt dobu trvání přechodu. Podle obrázku je D / a = v₀Δt / (a – r₀) = vΔt / (a – r). Z rovnosti 2. a 3. výrazu plyne a = (vr₀ – v₀r) / (v – v₀) . Z rovnosti 1. a 2. výrazu za použití předchozí rovnice dostaneme Δt = D(r₀ – r) / (vr₀ – v₀r). Dosazením v₀ = 2πr₀ / T₀, v = 2πr / T dostaneme konečný výsledek Δt = D(r₀ – r) / (2πr₀r) T₀T / (T₀ – T) = 7,93 h = 7 h 56 min.
3. Hledáme dobu ΔT, po jejímž uplynutí se Země a Venuše opět ocitnou na polopřímce s počátečním bodem ve středu Slunce. Platí 2πΔT / T = 2πΔT / T₀ + 2π, ΔT = T₀T / (T₀ – T) = 584 dnů. Pokud by byly splněny zjednodušující podmínky, nastal by předcházející přechod 2. listopadu 2002.
4. Rovina trajektorie Venuše je vzhledem k ekliptice skloněna o úhel 3,4°, čímž se v době možného přechodu při pohledu ze Země Venuše většinou neocitne na pozadí slunečního disku, nýbrž nad ním nebo pod ním.

Text je zveřejněn se souhlasem ÚV FO ČR. Oficiální stránky Fyzikální olympiády ČR najdete na www.uhk.cz/pdf/katedra/fyzika/Olympid/ nebo na fo.cuni.cz.